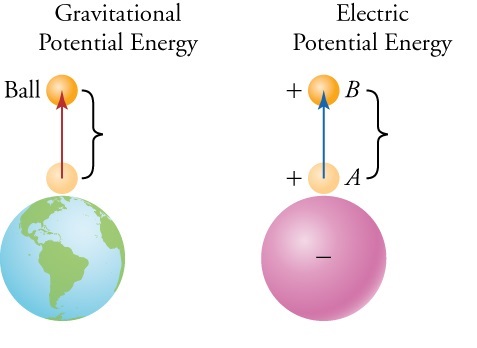
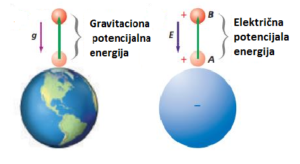
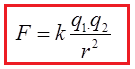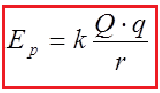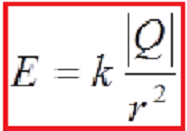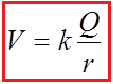Electric potential energy
Charges also have electrical potential energy. We learned that in work power energy chapter, objects have potential energy because of their positions. In this case charge in an electric field has also potential energy because of its positions.
Example: The ball is at a height h above the surface of the earth because of its own The position has gravitational potential energy. The charged body q is located in the electric field of charge Q, has energy called electric potential energy.
In other words, we can say that Energy required increasing the distance between two charges to infinity or vice verse. The potential energy of the electrified body is proportional to the amount of charge of the body. We use following formula to find the magnitude of electric potential energy.
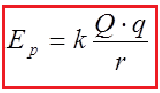
Electric potential energy is a scalar quantity and Joule is the unit of it 1J.
Work done by the electric field
If the force is a conservative, then the work done can be expressed in terms of a change in potential energy. Potential Energy of two point Charges.
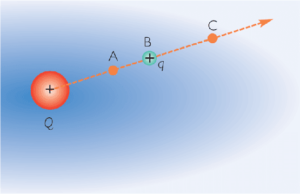
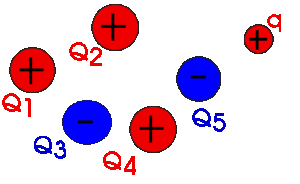
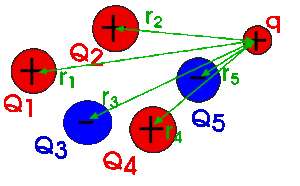
Example: Suppose we have two charges Q and q separated by A distance r. We now displace charge q along a radial line from point A to point B The force is not constant during this displacement.
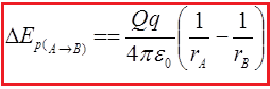
If the charged body moves opposite the electric field, then we say that some external force is working, the body moves opposite the lines of the electric field force. The work is negative, we get an increase in the potential energy of the moving body.

Example:
If we bring a charge Q from infinity and place it at point A the work done would be:
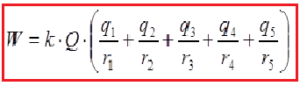
Electric Potential
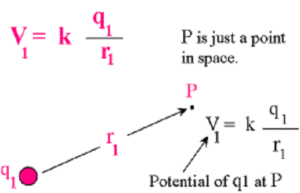
Electric potential is the electric potential energy per unit charge. It is known as voltage in general, represented by This is the electric potential due to a point charge r to a point charge.
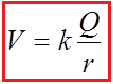
It has units of: 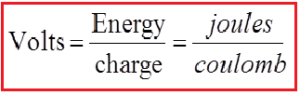
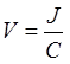
V is a scalar quantity. If q is negative then V becomes negative, or if q is positive then V becomes positive. This is called the electric field gradient. Thus the electric field also has units of Thus, the electric field also has units: ![]()
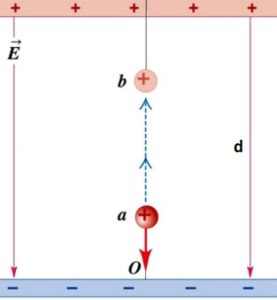
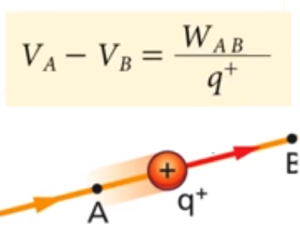
The potential difference between two points A, B in the field equals the work done against the field moving a unit positive test charge from point A to point B:
The potential difference is called the voltage
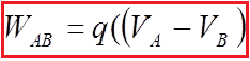
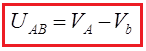
![]()
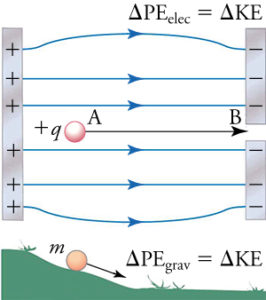
The positively charged body has a positive, while the negatively charged body has a negative potential. The electrons range from a lower point to a higher potential site.
The potential of the earth is taken as zero VE = 0. Thus, as a value for the electric potential the electric voltage is drawn between the body (T) and the Earth (E). UTZ = VT-VE = VT. The electrons from the Earth move to a positive charge, and are negatively charged particles are moving towards Earth.
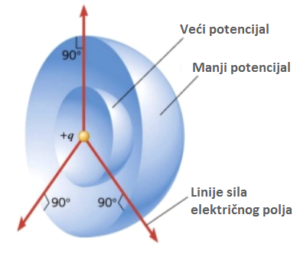
Equipotential surfaces
Thus, the electric potential is the same everywhere on this spherical surface). It is called an equipotential surface.
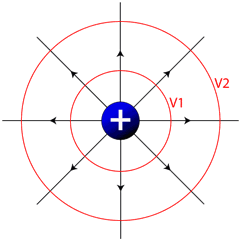
Equipotential surfaces are surfaces of constant potential
Electric field lines (black) and cross sections of equipotential surfaces (red) for (a) a uniform electric field, (b) the field due to a point charge, and (c) the field due to an electric dipole.
Potential of a Charged Sphere
Potential at surface is equal to the potential inside the sphere. Since there is no force acting inside the sphere, work is not done to bring the charge from surface to the inside of the sphere. As the distance from the surface of the sphere increase, potential decreases. Picture given below shows the change in the potential of the sphere inside, surface and outside. As you can see, potential is constant inside and surface of the sphere; however, it decreases with the increasing distance outside it.
Work Done by Uniform Electric Field
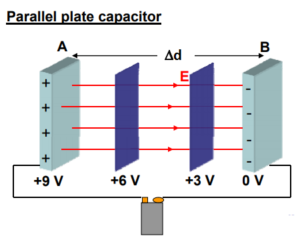
Example: The positive plate is at a potential of +9 V and the negative plate is at 0 V. What would the equipotential surfaces look like between the plates?
They would be a parallel set of planes!
Let the p py lates be separated by a distance Δd.
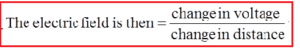
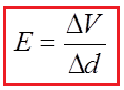
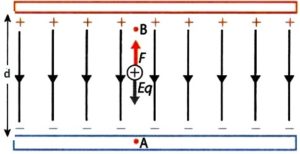
The strength of the electric field and the voltage or potential are the physical quantities by which we describe the electric field. There is a connection between them, and one can calculate one second size. We will report this connection to a homogeneous electric field. Work in moving the charge q in a homogeneous electric field between points A and B at a distance d is:
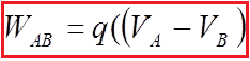
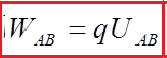
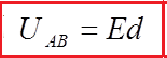
The electric field strength can be expressed over the voltage
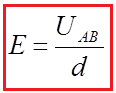
From this relationship we can derive a unit of electric field strength, volt per meter. She is equivalent to the newton unit per culon.
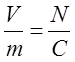
We now have 4 equations which kind of look similar: