Resistance
The electrical resistance of an electrical element measures its opposition to the passage of an electric current; the inverse quantity is electrical conductance, measuring how easily electricity flows along a certain path. Electrical resistance shares some conceptual parallels with the mechanical notion of friction. The SI unit of electrical resistance is the ohm (Ω).
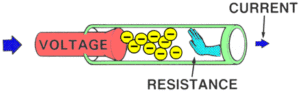
Resistance is the force that reduces the flow of electrons. Higher resistance decrease the flow of electrons and lower resistance allow electrons to flow freely.
Ohms Law states that when a voltage (V) source is applied between two points in a circuit, an electrical current (I) will flow between them encouraged by the presence of the potential difference between these two points. The amount of electrical current which flows is restricted by the amount of resistance (R) present. In other words, the voltage encourages the current to flow (the movement of charge), but it is resistance that discourages it.
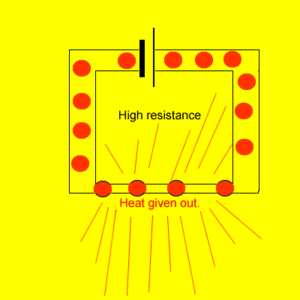
Current tends to create heat in high resistance wires. The electrons collide with stationary metal atoms and convert some of their kinetic energy into heat energy. The heating coil in a toaster or electric heater is made of high resistance wire. As current passes through the wire it quickly heats up and glows red hot.
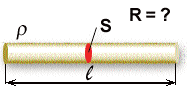
But the electrical resistance between two points can depend on many factors such as the conductors length, its cross-sectional area, the temperature, as well as the actual material from which it is made. For example, let’s assume we have a piece of wire (a conductor) that has a length L, a cross-sectional area A and a resistance R as shown.
The factors that affect resistance are
The factors that affect resistance are:
Temperature of resistance wire
Length of resistance wire
Thickness of resistance wire
Type of material of resistance wire
- Example 1: A Single Conductor The electrical resistance, R of this simple conductor is a function of its length, l and the conductors area, A. Ohms law tells us that for a given resistance R, the current flowing through the conductor is proportional to the applied voltage as I = V/R. Now suppose we connect two identical conductors together in a series combination as shown. Doubling the Length of a Conductor
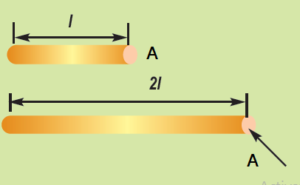
- Here by connecting the two conductors together in a series combination, that is end to end, we have effectively doubled the total length of the conductor (2l), while the cross-sectional area, A remains exactly the same as before. Therefore we can see that the resistance of the conductor is proportional to its length, that is: R ∝ l. In other words, we would expect the electrical resistance of a conductor (or wire) to be proportionally greater the longer it is.
- Example2: Doubling the Area of a Conductor Here by connecting the two conductors together in a parallel combination, we have effectively doubled the total area giving 2A, while the conductors length, l remains the same as the original single conductor. But as well as doubling the area, by connecting the two conductors together in parallel we have effectively halved the total resistance of the conductor, giving 1/2R as now each half of the current flows through each conductor branch.
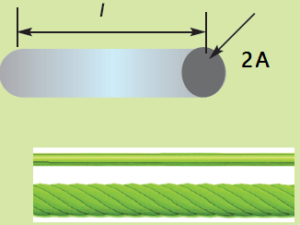
- Thus the resistance of the conductor is inversely proportional to its area, that is: R 1/∝ A, or R ∝ 1/A. In other words, we would expect the electrical resistance of a conductor (or wire) to be proportionally less the greater is its cross-sectional area. So hopefully we can see that the resistance of a conductor is directly proportional to the length (l) of the conductor, that is: R ∝l, and inversely proportional to its area (A), R ∝ 1/A. Thus we can correctly say that resistance is:
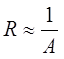
- Example3: Proportionality of Resistance But as well as length and conductor area, we would also expect the electrical resistance of the conductor to depend upon the actual material from which it is made, because different conductive materials, copper, silver, aluminium, etc all have different physical and electrical properties. Thus we can convert the proportionality sign (∝) of the above equation into an equals sign simply by adding a “proportional constant” into the above equation giving:
- The resistivity (ρ) of the material from which the conductor is made.
Wire Resistance
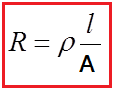
The resistance value of a wire depends on three parameters: resistivity, length and diameter. The formula to calculate wire resistance is as follows: In which R is the resistance (Ω), ρ is the resistivity of the material (Ωm), l is the length of the material (m), A is the cross-sectional area of the material (m2)
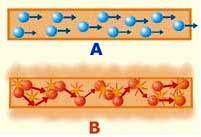
Why does Length affect resistance?The affect of length of a wire on resistance can beunderstood by looking at the atomic structure.Resistance is caused by electrons colliding with metal ions.When the length of the wire is increased, the electronshave to travel further. So the chance of collisions willincrease, causing the resistance to increase.
Why does Cross Sectional Area affect resistance? Increasing the thickness of a wire increases the cross sectional surface area that the electrons can flow through. This decreases the chance of collisions with metal ions. In thick materials the charge carrying particles are able to move through the conductor more easily, reducing resistance.
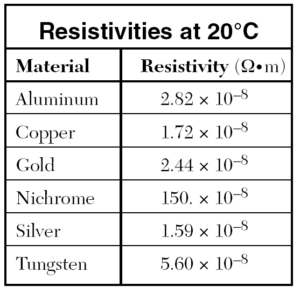
What is electrical resistivity?
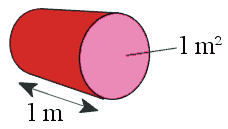
Electrical resistivity is a measure of a material’s property to oppose the flow of electric current. This is expressed in Ohm-meters (Ω⋅m). The symbol of resistivity is usually the Greek letter ρ (rho). A high resistivity means that a material does not conduct well electric charge. The electrical resistivity of a particular conductor material is a measure of how strongly the material opposes the flow of electric current through it. This resistivity factor, sometimes called its “specific electrical resistance”, enables the resistance of different types of conductors to be compared to one another at a specified temperature according to their physical properties without regards to their lengths or cross-sectional areas. Thus the higher the resistivity value of ρ the more resistance and vice versa. Resistivity is just a property of the conductor.Every material has a resistivity.It is actually the resistance of a 1m long piece of wire with across-sectional area of 1m2.
Materials such as copper and aluminium are known for their low levels of resistivity thus allowing electrical current to easily flow through them making these materials ideal for making electrical wires and cables. Silver and gold have much low resistivity values, but for obvious reasons are more expensive to turn into electrical wires.
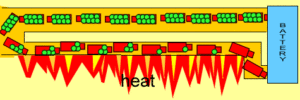
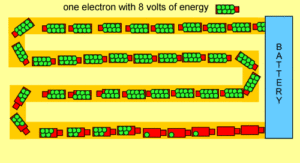
We read earlier that long wires have high resistance while short wires have low resistance. Lets revisit the analogy of electrons being tiny trucks carrying energy (voltage) out from the battery and through a wire. Look at the animation below. Trucks that travel though a long wire will use some of the energy they carry to help them move along the wire.
If each green bag represents one volt how many volts does each electron have as it leaves the battery?
As electrons travel though this long wire how many volts do they use to just move through the wire?
If the temperature of the resistance wire is too high, collisions will be high as both the electrons and atoms will be moving faster because of the increasing heat. This will increase the resistance.
