Gravitational Interaction

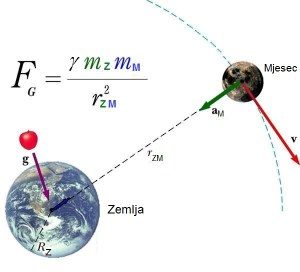
Gravity is an invisible force that draws all the bodies in the Universe to each other. Solar gravity keeps the planets in their orbits. Earth’s gravity ‘ensures’ that the Moon circulates in its orbit around the Earth. The gravitational force of other celestial bodies in the universe ‘keeps’ the Moon with a strong force so it does not collapse on Earth!

Jupiter is a very large planet which with its strong gravitational force is attracting smaller celestial bodies such as asteroids, meteor, and as such is protecting the Earth.

The gravitational force acts between the Earth and each body on its surface. Gravitational force is an attractive force between all bodies that have mass, and it acts even between the grains of sand. Gravitational attraction between two people also exists, but it has very low intensity so we do not feel it. Gravitational attraction becomes significant only when one of the bodies is very large, such as celestial bodies.

Newton’s Law of Gravity is in fact a mathematical description of a gravitational force or a gravitational interaction – the force that attracts two masses. Gravitation is a mutual attraction between the material bodies – the planets in the galaxies, the star in the universe, and so on.
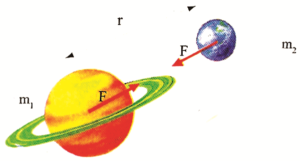
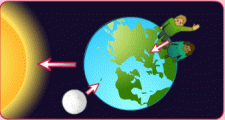 The strength of the gravitational force between the two bodies depends on the weight of these bodies and the distance between them. The force of attraction is stronger between the bodies whose masses are larger and the distance between them is smaller.
The strength of the gravitational force between the two bodies depends on the weight of these bodies and the distance between them. The force of attraction is stronger between the bodies whose masses are larger and the distance between them is smaller.
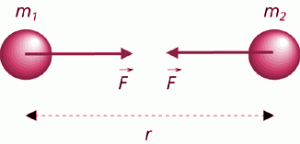
Gravitational forces are exclusively attractive forces and they also operate at a very large distances.
Newton’s law of gravity states:
The intensity of the force by which one body attracts the other is proportional to the masses of these bodies, and inversely proportional to the square of the distances between their centers.
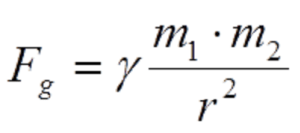 The constant γ is called a gravitational constant. If the body mass is 1 kg and the body is at a distance of one meter, it is:
The constant γ is called a gravitational constant. If the body mass is 1 kg and the body is at a distance of one meter, it is: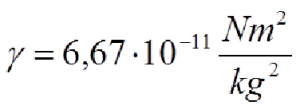
Example: gravitational interaction between the Earth and the Moon
The gravitational force that acts between two bodies is greater if the body mass is larger and the distance between the body is smaller.
Example: Two bodies have masses m1 = 1 t and m2 = 20 t, the distance between them is r = 10 m. What is the gravitational forces of these two bodies?
![]()
![]()
![]()
_________________
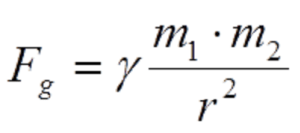
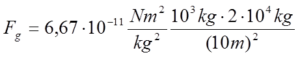
![]()
The gravitation does the following:
 – it pulls us towards the center of the Earth
– it pulls us towards the center of the Earth
– it pulls us back when we climb uphill
– it accelerates us when we go downhill
– it keeps the air cover around the Earth
– it is pushing the river to flow downstream
– it keeps the Moon in Earth’s orbit
– it keeps the planets in their orbits
– it keeps the sea in its troughs
Gravity field
 A space in which the effect of a gravitational force is felt by attracting one body to another can only be achieved through the material environment. This material environment (the form of matter) that exists throughout the body around the body and which acts on other bodies is called the gravitational field. In the space around the Earth there is a gravitational field through which the Earth attracts the bodies in it. The gravitational field is characterized by a considerable number of physical quantities, one of which is the gravitational field strength, which is the vector size. The gravitational field strength is numerically equal to the ratio of the gravitational force and the mass of the body. The field direction is the same as the direction of the gravitational force.
A space in which the effect of a gravitational force is felt by attracting one body to another can only be achieved through the material environment. This material environment (the form of matter) that exists throughout the body around the body and which acts on other bodies is called the gravitational field. In the space around the Earth there is a gravitational field through which the Earth attracts the bodies in it. The gravitational field is characterized by a considerable number of physical quantities, one of which is the gravitational field strength, which is the vector size. The gravitational field strength is numerically equal to the ratio of the gravitational force and the mass of the body. The field direction is the same as the direction of the gravitational force.
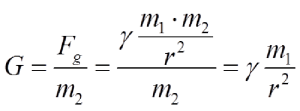
From the definition of a gravitational field is determined the unit of gravity strength field.
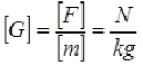
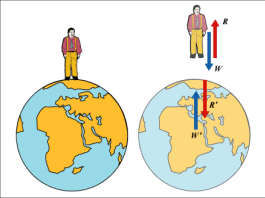
The earth attracts all the bodies that are located on it or in its vicinity with a force called the Earth’s gravity. This force is directed towards the center of the Earth. At low distances from the Earth’s surface, an attractive gravitational force can be considered:
![]()
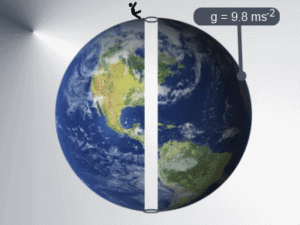
According to the second law of Newton, there is an acceleration, which is called the gravitational acceleration of the Earth denoted as “g”. At 45 ° latitude near the Earth’s surface, g = 9.81 m / s².
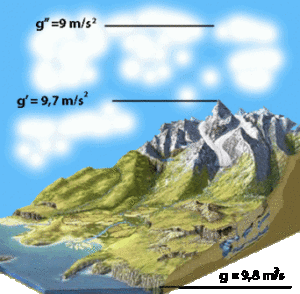
Gravitational acceleration on Earth is not the same at the poles and at the equator, and decreases with the distance from the center of the Earth,
Gravitational acceleration of celestial bodies depends on the mass of these bodies



Asteroids are very small and have little acceleration. Gravitational acceleration of the Sun is g = 274 m / s²; Moon g = 1.62 m / s²;



Pluto g = 0.17 m / s²; Neptune g = 11.4 m / s²; Uranus g = 9.0 m / s²



Saturn g = 11.1 m / s²; Jupiter g = 24.9 m / s²; Mars g = 3.73 m / s²;



Earth g = 9.81 m / s²; Venus g = 8.87 m / s²; Mars g = 3.73 m / s²; Mercury g = 3.70 m / s²;





Discovery of gravity is attributed to Isaac Newton who, after seeing an apple falling from the tree, came to the idea that the Earth attracted an apple with its gravitational force, just as it attracts the Moon to circle around it continuously as its satellite.
Newton knew that the celestial body in motion do not need any force to sustain it in that movement (Law of Inertia). In that case, the bodies would move in a straight line. Since the bodies move along the curved path, the cause for that may be some force which is pulling it towards the center of the path. Based on these assumptions, Newton has formulated the law of universal gravitation which, among other things, explains how with the action of the Earth’s gravitational force causes the Moon to circulate around the Earth, just like all the planets circle around the Sun. The closer the planet is to the Sun, the gravitational force of the Sun is stronger on it.