Area
The surface area represents a physical size of a body that is obtained by multiplying its length and width. Before calculating the surface area, it is necessary to measure the length and width of the rectangles. If it’s a square, it’s enough to measure just one of its pages. The surface is calculated according to the formula:
The SI unit for the area surface is 1 m2, which represents the area of the square of dimensions
one meter, as in Figure a.
The smaller units of the square meter are:
square decimeter (dm2) 1 dm2 = 10-2 m2
square centimeter (cm2) 1 cm2 = 10-4 m2
square millimeter (mm2) 1 mm2 = 10-6 m2
The larger units are:
ar (a) 1 a = 102 m2
hectare (ha) 1 ha = 104 m2
square kilometer (km2) 1 km2 = 106 m2
Volume
The volume (volumen) or space occupied by a body, is another physical size that we determine by calculation.
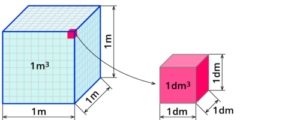
The unit for volume is one meter cubic meter (1m3).
This volume has a cube whose edge is 1 m long. Measurement of the volume as well as the surface is obtaned by measuring the length of a. The volume or size of the space it occupies is determined by the relation
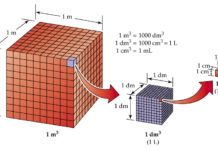
In practice the volume of liters (l) and milliliters (ml) are used for volume.
1l = 1 dm3 1ml = 1 cm3
One liter of volume corresponds to a volume of 1 dm3, while a milliliter corresponds to a volume of 1 cm3. hectolitre (hl) 1 hl = 100 l
deciliter (dl) 1 dl = 0.1 l
centilitar (cl) 1 cl = 0.01 l
milliliters (ml) 1 ml = 0.00 l
As you convert the volume units, remember that the cube has three dimensions (length, width and height) and that the ratio of meter and decimeters increases so that 1 m has 10 dm and in a cube of 1 m3 there is: 10 · 10 · 10 = 1000 dm3
Example: Calculate the area and volume of the cube in several steps: The dimensions of the cube are given in the figure:
After calculating the area surface of one of the sides, we calculate the surfaces of the other sides of the cube in the same way.
When we collect the surfaces of all of the cube sides we get the surface of the cube:
Volume is calculated by volume formula: