Newton’s Second Law is one of the basic laws of mechanics. And it speaks about how much acceleration a body mass m gets if the force F is affected by it. The body moves at a constant speed or is it at rest if there is no force acting on it. If the force of a certain mass acts on the body, the body will move rapidly.
Newton’s Second Law determines the relationship between force, mass, and acceleration, and also defines from what the acceleration depends on.
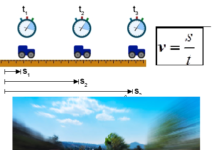
What the acceleration depends on, we can see in the following examples (first when the mass of the body is constant, and second when the force with which we act increases):
Example 1:
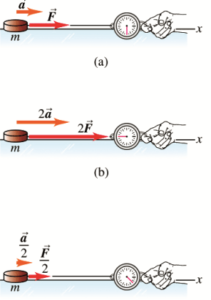– The body of the mass (m) is attached to the dynamometer and dragged on the surface.
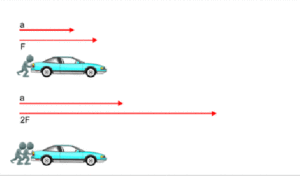
Figure (a): when the force F acts on the body’s mass m, the body gets some acceleration a.
Figure (b): when twice as strong force acts on the mass of the body, the acceleration of the body will increase proportionally to the force and the body will have acceleration 2a.
Figure (c): when a force whose strength is F / 2, half the strength in relation to the image (a). The body will proportionally reduce force, have less acceleration a / 2.
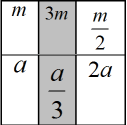
Example 2:
– When we want to examine how the acceleration of the body depends on the mass, we act with force of the constant strength, but at the same time we change the body’s mass.
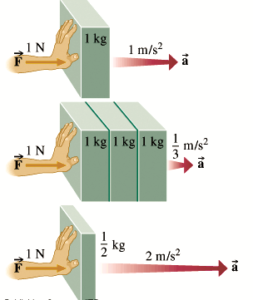In the figure, we can see that if on the body that weighs 1kg we act with the force of 1N intensity, the body will receive an acceleration of 1m/s². When the mass is three times higher and we act force F = 1N, the acceleration of the body will be reduced three times, it will be a = 1/3 m/s².
In the event that the mass is reduced to half a kilogram and we act with force of F = 1N, the acceleration will increase in this case two times.
Thus, we can conclude that acceleration in the case of the force of the same strength decreases when the mass of the body increases and vice versa.
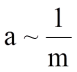
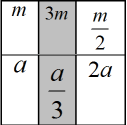
The acceleration that a body receives when a force acts on it, is proportional to the intensity of the force, and vice versa in proportion to the body mass.
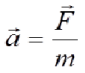From this we can conclude that the force gives acceleration to the mass.
The force acting on a body is equal to the product of the body’s mass and the acceleration that the body receives due to the action of that force. This law is called the Law of the Effect of Force.
The unit of force is Newton (N)
That is, the intensity of the force acting on a body is equal to the product of the mass of the body and the acceleration rate that the body receives due to the action of that force.
Inertia is the body’s ability to resist the change in velocity due to the action of force. The mass of the body is a measure of body inertion.
Example: What is the intensity of the force acting on a 5 kg carriage, from which the carriage gets an acceleration of 2 m/s²?
m = 5 kg
a = 2 m / s²
—–
F =?
F = ma = 5 kg. 2 m / s² = 10 N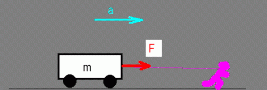 
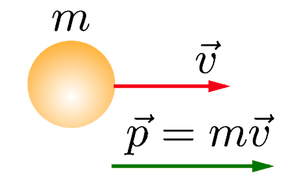What happens to the impulse of the body when a force acts upon it for some time? The impulse of the body changes under the influence of force. Since the body’s impulse depends on the speed and the force causes that change,
the impulse of the body changes due to the action of that force.
Example: In the picture below we can see the white ball and the red ball in front of it. Both balls are at rest. Since v = 0, the impulse of the balls is equal to zero. If we apply a force on the white ball by using a stick, it will cause it to move and strike the red ball, which will change the speed of the white ball and impulse. Also the speed of the red ball, which was up to that point at rest, will be also changed.
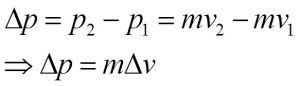The amount of impulse change of the body Δp and the time for which this change occurred Δt is called the rate of change in body pulses.
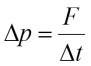
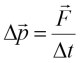The speed of the change in the impulse of the body is equal to the force acting on that body and is carried out in the direction of the action of this force.
The relationship between the change in the impulse of the body and the force that induces this change was studied by Newton: This formula is called the Newton’s Second Law.
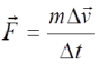The rate of change in the body’s impulse is equal to the force acting on that body and is carried out in the direction of the action of that force. The ration of change of the body’s impulse and the time interval is equal to the resulting force that acts on that body during that time interval.
The magnitude Δp = FΔt is called the impulse of the force. The impulse of the force is always equal to the impulse of the body.
The Newton’s Second Law is a natural law that connects the state of movement of the body, or the accelerated movement of the body, with the force acting on it and with a mass as a measure of resistance, change the state of movement of that body.
