Slaganje sila istog pravca
Obično na jedno tijelo nikada ne djeluje samo jedna sila. Na nas dok se krećemo djeluje sila Zemljine teže i otpor vazduha. Kada na tijelo djeluju više od jedne sile, njihovo djelovanje možemo zamjeniti samo jednom silom. Sila koja svojim djelovanjem može zamijeniti djelovanje dviju ili više sila zove se rezultujuća sila ili rezultanta.
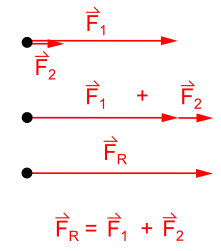
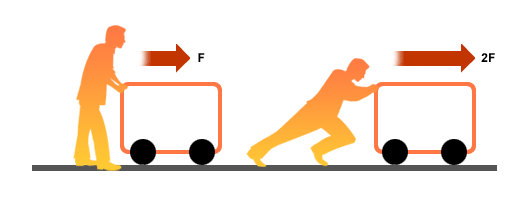
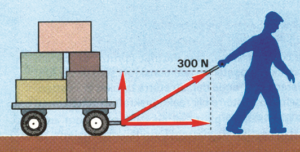
Primjer: Sanduk guraju dva radnika, pri čemu svaki od njih djeluje izvjesnom silom i to F1 i F2 . Isti predmet može gurati jedan snažniji čovjek silom F. U ovom slučaju djelovanje dvije sile zamijenili smo jednom silom.
Određivanje rezultante Fr sila F1 i F2 je slaganje sila, a sile F1 i F2 su komponente sile F. Ako dvije sile djeluju u jednom pravcu i njihova rezultanta će djelovati u istom pravcu kao i komponente sila. U prethodnom primjeru sile i F1 i F2 djeluju u istom pravcu i istom smjeru. Rezultujuća sila se dobija vektorskim sabiranjem. Ovakav zbir se naziva vektorski ili geometrijski zbir. Rezultanta sila istog pravca i smjera jednaka je zbiru intenziteta tih sila. Ima isti pravac i smjer kao komponente.
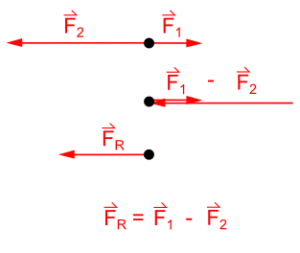
Slaganje sila is tog pravca suprotnog smjera . Dvije sile F1 i F2 djeluju u različitim smjerovima. Intenzitet rezultante ovih sila jednak je razlici intenziteta sila F1 i F2. Smjer odgovara smjeru sile koja ima veći intenzitet.
Intenzitet rezultante sile istog pravca suprotnog smjera jedn aka je razlici intenziteta tih sila. Ima smjer veće sile.
Slaganje sila pod uglom
Sile koje djeluju na istu tačku Ako dvije sile imaju zajedničku napadnu tačku i djeluju pod uglom, njihovo djelovanje možemo zamjeniti rezultujućom silom.
Primjer: Kada na tijelo djelujemo sa dvije sile (slika 1) koje imaju istu napadnu tačku, pod pravim uglom. Djelovanje ove dvije sile mogu se zamjeniti rezultujućom silom (slika 2) koja ima pravac dijagonale ovog paralelograma.
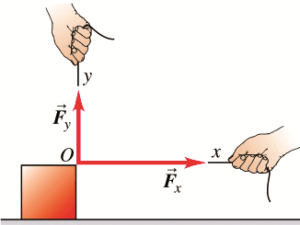
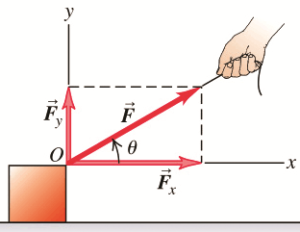
Rezultanta dvije sile koje djeluju na tijelo pod uglom, a imaju istu napadnu
tačku, po intenzitetu je jednaka brojnoj vrijednosti dijagonale paralelograma.
Stranice dijagonale odgovaraju komponentama sila, rezultanta ima pravac
dijagonale.
Sile koje se sijeku u jednoj tački.
Ako postoje dvije sile koje djeluju na neko kruto tijelo, a odsječci prava koje ih sadrže se sijeku u jednoj tački, treba da pomjeramo obje strelice sile po njihovim pravama tako da se poklope napadne tačke da bismo našli rezultantu. Kada to postignemo, onda tražimo rezultantu isto kao u slučaju dvije sile koje djeluju na istu tačku.
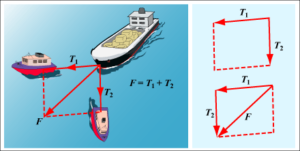Primjer: Dva remorkera čeličnim užadima vuku brod. Brod se kreće kao da ga vuče samo jedna sila od tačke koja se nalazi između dva užeta. Na slici je ova sila dijagonala paralelograma obojena zeleno.
Razlaganje sila
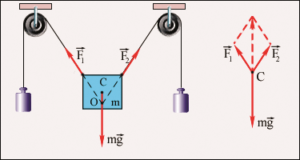
Djelovanje više sila smo predstavili preko rezultujuće sile isto tako djelovanje jedne sile možemo pokazati preko djelovanja njenih komponenti. Razlaganje sila možemo posmatrati preko paralelograma gdje se sila koja se razlaže uzima kao dijagonala paralelograma. Dvije stranice paralelograma koje grade ugao tjemena dijagonale predstavljaju komponente sila.
Primjer: Težina velikog tega se razlaže na dvije komponente, dva manja tega.
Ravnoteža sila
Kada su sile koje djeluju na tijelo u ravnoteži tada ono ne mijenja svoj položaj. Ako je rezultujuća sila koja djeluje na neko tijelo jednaka nuli tada kažemo da su sile koje djeluju na tijelo u ravnoteži.
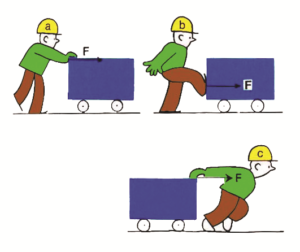
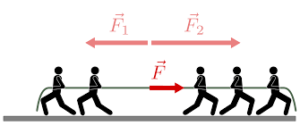
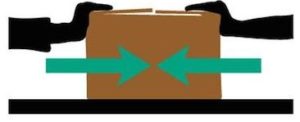U svakodnevnom životu postoji mnogo situacija za ravnotežu sila. On djeluje silom na suprotnu stranu. U stanju mirovanja su sile istog intenziteta samo suprotnog smjera koje međusobno djeluju. Na slici b dva dječaka djeluju jedan na drugog silama istog intenziteta suprotnog smjera. Rezultat je mirovanje jednog i drugog zbog toga što su sile kojim međusobno djeluju u ravnoteži. Ako na jedno tijelo djeluju dvije sile istog intenziteta i pravca a suprotnog smjera, rezultujuća sila biće jednaka nuli. Za ovakvo tijelo kažemo da je u ravnoteži.
Primjer: Ako na tijelo djeluju dvije sile u suprotnim smjerovima, a intenzitet im je isti. Njihova rezultanta biće jednaka nuli.
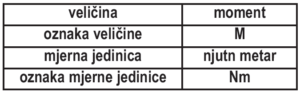
Moment sile
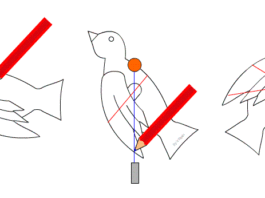
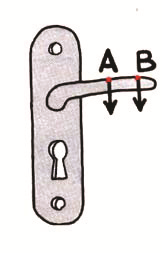Jedna od važnih fizičkih, veličina, čije je poznavanje važno za razumijevanje ravnoteže tijela jeste moment sile. Uhvatimo kvaku sa slike u tački A, zatim u tački B i pri tome djelujemo istom silom. Možemo odmah uočiti da je lakše otvoriti kvaku ako uhvatimo u tački B. Dakle efekat koji želimo postići ne zavi-si samo od jačine sile kojom djelujemo već i od njenog rastojanja od napadne tačke te sile.
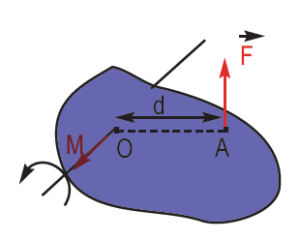
Okretanje kvake oko tačke O zavisi od sile F, i njenog normalnog rastojanja d od ose rotacije. Normalno rastojanje d od ose rotacije do pravca djelovanja sile naziva se krak sile. Proizvod kraka sile d i njenog intenziteta zove se moment sile M.
M = F . d
Moment sile definisan gornjom relacijom je vektorska veličina koju karakteriše intenzitet M koji je brojno jednak proizvodu kraka sile i njenog intenziteta. Jedinica za moment je (Nm).
