STRUKTURA PROBLEMSKE NASTAVE

PROBLEM1:

Kako možete u toku par sekundi da smanjite svoju težinu?

Odgovor: Uđite u lift, stanite na vagu i mjerite masu koju vaga pokazuje  kada lift miruje, kad se kreće vertikalno naviše i ubrzano krene vertikalno naniže, pogledajte vagu i vidjećete kad kazaljka pokazuje najmanju vrijednost.

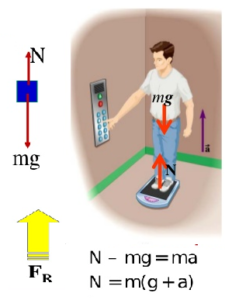
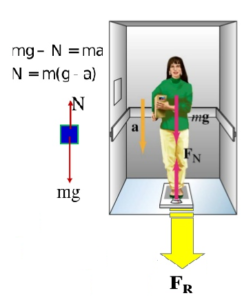
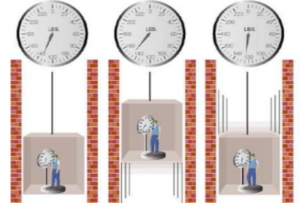
Naravno, ovdje nije riječ o smanjenju mase tijela, nego o smanjenju težine kao sile kojom pritiskate vagu. Slika ispod pokazuje pomjeranje kazaljke u sva tri slučaja i slučaj kad je vaša težina najmanja:

PROBLEM2:

Plivač u odnosu na obalu brže pliva niz rijeku nego kada pliva suprotno toku rijeke.

Kada plivač brže pređe rastojanje od tačke A do tačke B i natrag, od B do A:

– u rijeci ili

– u mirnoj vodi jezera?

Odgovor: Ako su rastojanje od A do B,  v brzina toka rijeke u odnosu na obalu, a V brzina plivača u odnosu na vodu rijeke. Pretpostavka je da je,  za kretanje od A do B i od B do A u rijeci, plivaču je potrebno vrijeme:

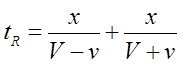
a isto rastojanje prelazi u jezeru za vrijeme:

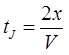
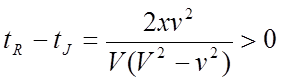Slijedi, plivač brže pređe rastojanje od A do B i nazad do A u mirnoj vodi jezera nego u rijeci. Zaključak je da plivač više vremena »potroši« plivajući uz rijeku nego što »uštedi« plivajući niz rijeku. U jezeru je plivaču za kretanje od A do B potrebno isto vrijeme kao i za kretanje od B do A.

Na pokretnim stepenicama se može izvesti jednostavan eksperiment koji potvrđuje dobijeni rezultat.

PROBLEM 3:

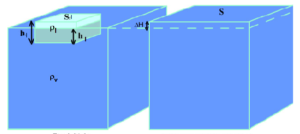
U sudu do vrha napunjenom vodom, pliva parče leda.

Kako će se promijeniti nivo vode u sudu kada se čitav led istopi?

Važi li isti odgovor ako se u ledu nalazilo:

1. parče plute,
2. metalni šaraf?

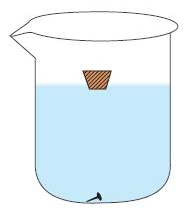Odgovor: Kada led pliva u vodi onda na njega djeluje sila potiska jednaka sili teže koja djeluje na njega. Kada se led istopi, onda on prelazi u vodu iste zapremine kolika je, prema Arhimedovom zakonu, zapremina vode koju je led bio istisnuo. Slijedi, nivo vode se neće promijeniti.

Postojanje plute u ledu neće promijeniti odgovor: pluta će nastaviti da pliva u vodi istiskujući dio vode na koju djeluje sila teže jednaka sili teže koja djeluje na plutu.

Metalni šaraf poslije topljenja leda potone na dno suda. Na dio vode koju tada istiskuje šaraf djeluje manja sila teže nego na šaraf, a prije topljenja leda šaraf je »učestvovao« u istiskivanju onoliko vode na koju djeluje sila teže kao i na šaraf. Slijedi, nivo vode će se sniziti.

PROBLEM 4:

Lopta je izbačena vertikalno uvis. Koje je vrijeme duže: penjanja ili spuštanja?

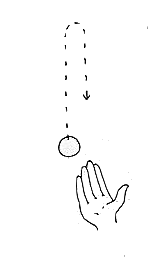
Odgovor: U ovom slučaju nije eksplicitno navedeno da se otpor vazduha može zanemariti, pa je kinetička energija lopte na kraju leta manja nego na početku. Takođe, na bilo kojoj visini, brzina lopte je manja pri spuštanju nego pri podizanju. Odavde je jasno da je vrijeme penjanja kraće od vremena spuštanja.

PROBLEM 5:

Iz vazdušnog balona, sa velike visine iznad zemljine površi, ispuštena je gumena lopta. Lopta padne na zemlju i odbije se od nje. Koliko je ubrzanje lopte neposredno poslije odbijanja?

Napomena: Pogrešan je “očigledan” odgovor: ubrzanje zemljine teže.

Odgovor: Proporcionalno povećanju brzine lopte raste i sila otpora vazduha tako da lopta veoma brzo, zbog izjednačavanja intenziteta sile otpora i sile zemljine teže, počne da se kreće stalnom brzinom.

Neposredno poslije odbijanja lopte ove dvije sile imaju ne samo jednake intenzitete već i isti smjer.

Slijedi, tada je ubrzanje lopte dva puta veće od ubrzanja zemljine teže.

PROBLEM 6:

Jedan kraj daske dužine 10 metara je na cilindru, a drugi kraj drži čovjek, kao na slici. On je gura naprijed a cilindar se kotrlja bez proklizavanja po horizontalnoj podlozi. Takođe, nema ni klizanja između daske i cilindra. Daska je čitavo vrijeme horizontalna.

Koliko rastojanje treba da pređe čovjek dok drugi kraj daske ne dođe do cilindra?

Napomena: Pošto se cilindar kotrlja bez klizanja po podlozi onda duž kojom cilindar dodiruje dasku kreće se dva puta većom brzinom od brzine kretanja ose cilindra. Zbog toga, kada čovjek pređe 10 metara, onda će osa cilindra biti ispred njega na rastojanju od 5 metara. Kada pređe još 5 metara, osa cilindra će mu biti na rastojanju od 2,5 metara itd. Hoće li čovjek uopšte i doći do cilindra?

Matematičari rješenje ovog zadatka obično svode na izračunavanje granične vrijednosti zbira beskonačno mnogo razlomaka čiji je brojioc dužina daske a imenioc redom brojevi: 1, 2, 4, 8, 16, 32, …

Odgovor:

Neka je  dužina daske D, a  C rastojanje koje pređe osa cilindra do trenutka kada drugi kraj daske dođe do njega. Pošto je brzina daske u odnosu na podlogu dva puta veća od brzine ose cilindra, onda je:

Tj. C=D. Prema tome, čovjek treba da pređe 20 metara. Zadatak se može elegantnije riješiti u sistemu referencije »vezanom« za dasku. U tom sistemu osa cilindra se kreće prema čovjeku brzinom istog intenziteta kao i u sistemu »vezanom« za podlogu i za određeno vrijeme pređe 10 metara, tj. stigne do drugog kraja daske. Za isto vrijeme čovjek, čija je brzina dva puta veća, pređe 20 metara.

PROBLEM 7:

Sunce se pri izlasku pojavilo na Istoku u 7 sati. Poznato je da se Sunčevi zraci od Sunca do Zemlje „putuju“ 8 minuta. Ako bi oni rastojanje od Sunca do Zemlje prelazili trenutno, Sunce bi se na Istoku pojavilo 8 minuta ranije.  Da li je ovo tačno?

Odgovor: Nije tačno.

Zemlja se uvijek nalazi u prostoru koji je osvijetljen i obrće se oko svoje ose, pa brzina prostiranja Sunčevih zraka ne utiče na izlazak i zalazak Sunca.

PROBLEM 8:

Možete li čovjek podići jedan kubni metar plute?

Odgovor: Masa kubnog metra plute je 240 kg. Procijenite sami da li možete podići toliki teret.

PROBLEM 9:

Kako pomoću lenjira odrediti silu potiska koja djeluje na kvadar koji pliva na vodi?

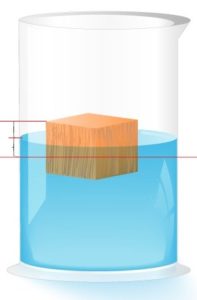
I način. Izmjeriti lenjirom dimenzije kvadra i izračunati zapreminu tijela (V). Staviti tijelo u vodu, izmjeriti visinu dijela tijela iznad vode i izračunati zapreminu ovog dijela tijela (V). Sila potiska je tada:

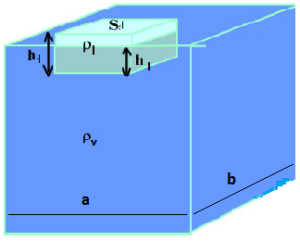
II način. Naći razliku nivoa vode u posudi kada je tijelo van vode (h1) i u vodi (h2). Zapremina uronjenog dijela tijela je tada, a sila potiska:

gdje su a i b  dužina i širina unutrašnjeg dijela posude.

PROBLEM 10:

Gustina sirovog krompira je malo veća od . Zašto u skladište čija je zapremina ne može da stane više od 700kg  sirovog krompira?

Odgovor: Zato što je prostor između krompira ispunjen vazduhom.

PROBLEM 11:

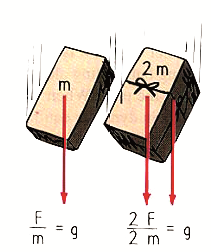
Jedan učenik tvrdi da cijela cigla (ako se zanemari otpor vazduha) padne s neke visine na tlo dvostruko brže od pola cigle, zato što je Zemlja privlači dva puta većom silom. Drugi učenik tvrdi da će cijela cigla pasti dva puta sporije, zato što je njena inertnost dvostruko veća od polovine cigle. Ko je u pravu?

Odgovor: Ni jedan ni drugi. Riječ je o slobodnom padu pri kojem obije cigle imaju jednako ubrzanje i padnu za isto vrijeme na tlo. Sto pokazuje i slika ispod.

PROBLEM 12:

 Sila kojom Sunce privlači Mjesec je dva puta veća od sile kojom Sunce privlači Zemlju. Zašto je Mjesec satelit Zemlje, a nije samostalna planeta?

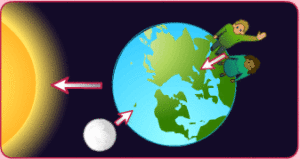
Odgovor: Sunce „saopštava“ Mjesecu i Zemlji jednaka ubrzanja. Zato Mjesec i Zemlja čine jedan sistem od dva nebeska tijela koja se kreću oko zajedničkog centra mase. Centar mase sistema Zemlja-Mjesec rotira oko Sunca.

PROBLEM 13:

Zašto ne primjećujemo kretanje Zemlje oko Sunca iako je njena brzina skoro 30 kilometara u sekundi?

Centripetalno ubrzanje usljed rotacije Zemlje oko Sunca () je zanemarljivo malo u odnosu na ubrzanje slobodnog pada ().

PROBLEM 14:

Poznato je da je sila teže na Mjesecu 6 puta manja nego na Zemlji. Da li to znači da bi skakač uvis – koji na Zemlji preskače visinu 2 m – na Mjesecu mogao da preskoči 12 m?

Odgovor: Sportista neće moći da preskoči 12m.

Težište sportiste prije skoka nalazi se na visini oko 1m, a u trenutku prelaska preko grede na visini od, 2,1m  tj. podigne se za 1,1m. Ulaganjem iste energije na Mjesecu, sportista će podići svoje težište na visinu 1,1x 6 = 6,6m i preskočiti gredu postavljenu na 1m + 6,6m =7,6m.

PROBLEM 15:

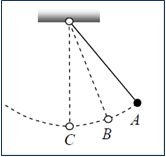
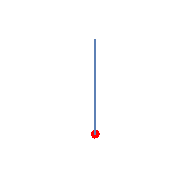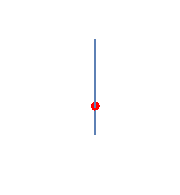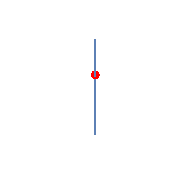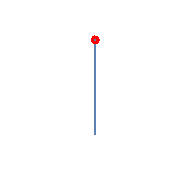
Kuglica je obješena o nit i osciluje kao matematičko klatno. Najvisočija tačka do koje dolazi kuglica je tačka A.

Kako je usmjeren vektor ukupnog ubrzanja kuglice u tačkama A, B, i C?

Odgovor: U tački A kuglica se trenutno zaustavi. Tada je njeno normalno ubrzanje jednako nuli i ostaje samo tangentno ubrzanje koje je usmjereno u pravcu tangente na putanju (slika A).

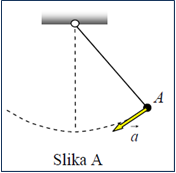
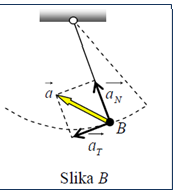
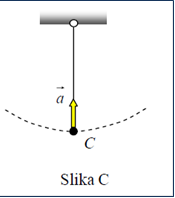
U tački  B kuglica ima i tangentno i normalno ubrzanje. Pravac ukupnog vektora ubrzanja kuglice prikazan je na slici B.

U tački C brzina kuglice je maksimalna (više ne raste, a nije počela da se smanjuje). Tada je tangentno ubrzanje jednako nuli (slika C), a ukupno ubrzanje je jednako normalnom ubrzanju kuglice (usmjerenom ka centru kružnice).

PROBLEM 16:

Na sva tijela na Zemlji djeluje privlačna sila Sunca. U toku noći ta sila ima isti smjer kao i privlačna sila Zemlje, a u toku dana – suprotan. Da li to znači da su tijela teža noću nego danju?

Ne – privlačna sila Sunca djeluje ne samo na tijela na Zemlji nego i na Zemlju, saopštavajući im isto ubrzanje. Zbog toga – privlačenje Sunca ne utiče na pokazivanje vage.

PROBLEM 17:

Neka imate tri provodne kugle: jednu negativno naelektrisanu (A) i dvije nenaelektrisane (B i C). Kako pomoću kugle A, ne mijenjajući njeno naelektrisanje, možete naelektrisati druge dvije kugle: kuglu B pozitivno, a kuglu C negativno?

Učvrstite kugle  B i C za odvojene podloge od izolatorskog materijala. Zatim postavite ove dvije kugle tako da se dodiruju, a kuglu A približite kugli B. I, na kraju, odmaknite kugle B i C.

PROBLEM 18:

Na dno prazne posude neprovidnih zidova dječak je stavio kuglicu, a zatim se malo odmaknuo da kuglicu više ne vidi (slika).

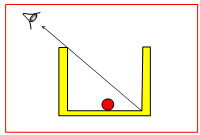
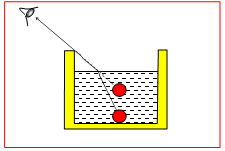
Međutim, kada je napunio posudu vodom, on je vidio kuglicu. Zašto?

Odgovor: Opisani eksperiment tumačimo prelamanjem svjetlosti. Pri prelasku iz vode u vazduh svjetlosti zraci se prelamaju (slika). Zbog toga naše oko vidi lik kuglice na produžetku prave linije koja prolazi kroz oko i tačku u kojoj svhetlosni zrak izlazi iz vode.

PROBLEM 19:

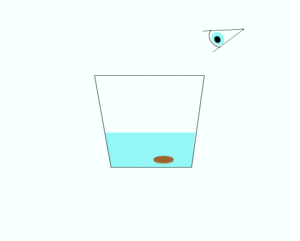
U kalorimetru se nalaze dva sloja iste tečnosti: dolje hladna, a iznad – topla. A) Hoće li se promijeniti zapremina ukupne tečnosti kada se uspostavi termička ravnoteža?

1. B) Kakav je odgovor u slučaju da su u sudu voda mase m1 i temperature 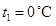i voda mase m2  i temperature  () ?

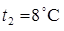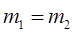Odgovor:

1. A) Neće se promijeniti;
2. B) Temperatura termičke ravnoteže je 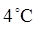, a pri ovoj temperaturi voda ima najveću gustinu (»anomalija vode«). Zbog toga će se zapremina vode u sudu smanjiiti kada dođe do termičke ravnoteže.

PROBLEM 20:

Da li je masa vazduha u prostoriji u kojoj se nalazite veća od mase vašeg tijela?

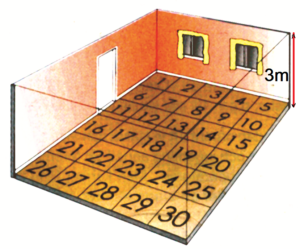
Odgovor: Potrebno je da prvo procijenite dimenzije (u metrima) prostorije u kojoj se nalazite i izračunate zapreminu te prostorije. Kada dobijenu zapreminu pomnožite sa gustinom vazduha (1,3 kg/m³), vidjećete da li je veća masa vazduha ili masa vašeg tijela.

PROBLEM 21:

Može li se cjelokupno naelektrisanje jednog provodnika prenijeti na drugi provodnik?

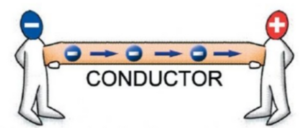
Može – kada se naelektrisani provodnik postavi u unutrašnjost nenaelektrisanog provodnika a oba provodnika su u kontaktu.

PROBLEM 22:

Šta je teže u vazduhu: 100 kg drveta ili 100 kg gvožđa?

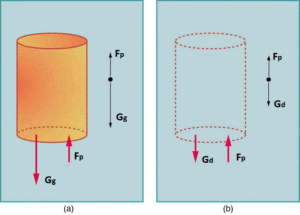
Odgovor: Zapremina drveta je veća od zapremine gvožđa više od 8 puta, a toliko puta je veća i sila potiska kojom vazduh djeluje na drvo. Slijedi, 100 kg drveta je lakše od 100 kg gvožđa.

PROBLEM 23:

Umjetnik je nactao crtež „Zimski ravničarski pejzaž“.

U kojem dijelu planete Zemlje je on mogao da posmatra ovakvu prirodu?

Odgovor: Ne postoji mjesto sa kojeg je umjetnik mogao da posmatra ovakvu prirodu.

Mjesec može da bude okrenut “rogovima” naviše samo u mjestima blizu ekvatora, a pejzaž na crtežu je zimski! Tačno je da snijega ima i u blizini ekvatora u visokim planinama, ali, predio na crtežu je – ravničarski.

PROBLEM 24:

Tijelo je potpuno potopljeno u tečnosti. Gdje djeluje sila potiska: u težište potopljenog tijela ili u težište tijelom istisnute tečnosti?

         Sila potiska uvijek djeluje u težište tijelom istisnute tečnosti, a ne u težište potopljenog tijela. U opštem slučaju se ove dvije tačke ne poklapaju.

Neka je nehomogeno lopta napravljena od bakra (dio lopte prikazan bijelom bojom na slici) i drveta.

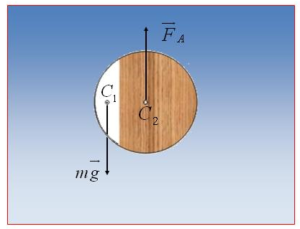
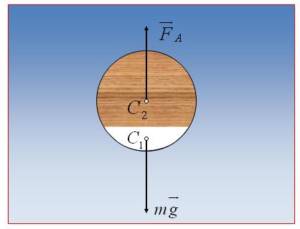
Odgovor: Sila teže djeluje u težište tijela (C₁), a sila potiska u težište tijelom istisnute tečnosti (C₂). Pod dejstvom ove dvije sile, lopta će zauzeti položaj prikazan na drugoj slici.

Od odnosa intenziteta sile teže i sile potiska zavisi da li će lopta da pliva, lebdi ili tone.

PROBLEM 25:

Kada se dva kvadra, A i B, jednaka po veličini i obliku, stave na terazije, onda terazije pokazuju da kvadar A ima veću težinu od kvadra B.

Ako se ova dva kvadra zalijepe i postave na ivicu trostrane prizme, onda “preteže” kvadar B.

Kako je to moguće?

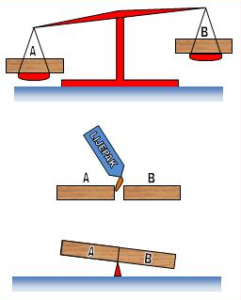
Odgovor: Kvadar B, čija je masa, kao što pokazuju terazije, manja od mase kvadra A, ima šupljinu na čijem je kraju parče bakra.

Zbog toga je težište kvadra B više udaljeno od tačke oslonca (geometrijske sredine) i moment njegove sile teže u odnosu na vrh trostrane prizme je veći nego kvadra A.

PROBLEM 26:

Kako se može odrediti masa predmeta veća od 1 kg (na primjer, plastična boca napunjena pijeskom)? Na raspolaganju je pribor: dinamometar opsega do 4 N, tanka neistegljiva nit dužine 1 m, milimetarski papir i stativ.

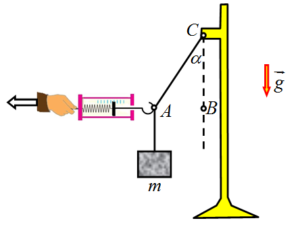
Odgovor: Tijelo treba objesiti kao na slici, a dinamometrom povući nit u horizontalnom pravcu.  Pomoću milimetarskog papira može se odrediti odnos dužina dvije duži  (tangens ugla ).

Za vrijednost sile F koju pokazuje dinamometar, masa tijela je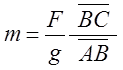  

PROBLEM 27:

Kako se može odrediti masa predmeta manja od 10 g (na primjer, plastična alka)? Na raspolaganju je pribor: dinamometar podjeljka 0,5 N, tanka neistegljiva nit dužine 2 m, milimetarski papir i dva stativa.

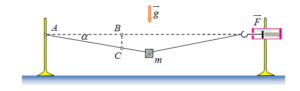
Jedan kraj niti treba pričvrstiti za jedan stativ, a drugi kraj niti povezati sa dinamometrom u horizontalnom položaju. Dinamometar treba da je čvrsto privezan za stativ. „Horizontalnost“ niti se provjerava milimetarskim papirom. Zatim se predmet okači za sredinu niti, kao na sl.

Odgovor:  Pomoću milimetarskog papira može se odrediti odnos dužina dvije duži (tangens ugla između horizontalnog pravca i naklonjenog dijela niti). Ako dinamometar pokazuje vrijednost sile F , onda je masa tijela:

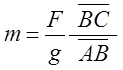
PROBLEM 28:

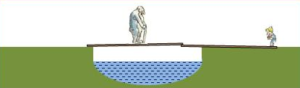
Unuk i đed treba da pređu preko kanala: jedan sa desne strane na lijevu, a drugi u suprotnom smjeru. Sa obje strane kanala postoji po jedna daska, ali je njihova dužina kraća od širine kanala. Na koji način đed i unuk mogu da pređu sa jedne strane kanala na drugu?

Odgovor: Oni treba da postupe na način prikazan na slici. Prvo treba đed da pređe preko dasaka i stane na mjesto unuka, a zatim unuk da pređe preko „mosta“.

PROBLEM 29:

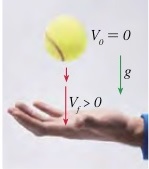
Potrebno je da se odredi početna brzina kuglice koja izleti iz dječijeg pištolja-igračke. Kako se to može uraditi pomoću štoperice?

Usmjerimo igračku vertikalno naviše i izmjerimo vrijeme  od trenutka ispaljivanja do trenutka kada se kuglica vrati na visinu sa koje je izbačena. U najvišoj tački putanje kuglice, njena brzina je jednaka nuli, tj. , odakle je . Iz čega slijedi da je  , jer je kuglici potrebno isto vrijeme za kretanje naviše i naniže. Konačno, traženu brzinu računamo po formuli:

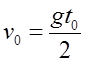
PROBLEM 30:

Odrediti vrijednost koeficijenta trenja između dva drvena predmeta ako su dati: drvena daska, drveni teg i lenjir.

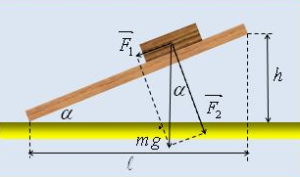
Odgovor: Stavimo teg na dasku i podižemo je dok teg ne krene. Sa slike vidimo da sila  F1 ima pravac paralelan pravcu daske i intenzitet  . Sila trenja između tega i daske je .

Pri ravnomjernom kretanju tega je:  

odakle za koeficijent trenja k dobijamo da je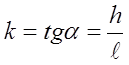 

Prema tome, za određivanje vrijednosti koeficijenta trenja k dovoljno je izmjeriti h  i l.

PROBLEM 31:

Na raspolaganju nam je drveni kvadar čija je jedna strana znatno veća od ostalih.

Kako pomoću jednog lenjira možemo odrediti koeficijent trenja između kvadra i stola?

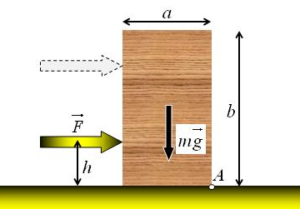
Odgovor: Kada na kvadar djelujemo horizontalnom silom intenziteta većeg od sile trenja  , na malom rastojanju h od njegove osnove, onda on počne da se kreće.

S druge strane, kada djelujemo istom silom na kvadar ali na većoj visini, može se desiti da se kvadar ne pomjera po stolu. To je u slučaju kada je moment sile , u odnosu na osu koja je normalna na ravan crteža i prolazi kroz tačku A , veći od momenta sile  u odnosu na istu osu: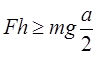 

gdje je a – širina kvadra.

Potrebno je odrediti visinu na kojoj se „nalazi“ sila kada predstavlja granicu između ova dva slučaja. Tada iz sistema jednačina;

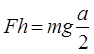
nalazimo da je koeficijent trenja k:

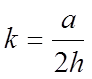Odavde se može zaključiti još i da je ovakvo određivanje koeficijenta trenja moguće samo u slučaju kada visina kvadra zadovoljava uslov:

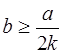
PROBLEM 32:

Kako se određuje brzina kišnih kapi po tragovima koje one ostavljaju po prozoru voza, koji se kreće koristeći brzinometar i uglomjer?

Odgovor: Ako se voz kreće s lijeva na desno brzinom , onda u odnosu na njega kapi imaju istu vrijednost brzine ali suprotno usmjerenu .

Osim toga, kišne kapi 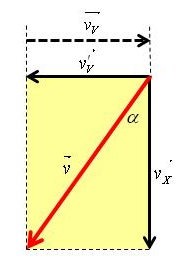se kreću vertikalno u odnosu na voz , brzinom , koju treba da odredimo. Vektor rezultantne brzine zaklapa ugao  sa vertikalnim pravcem i zadovoljava relaciju:

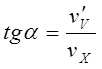Iz ovog izraza određuje se brzina padanja kišnih kapi:

Ugao izmjerimo uglomjerom.

Brzina  se izračunava tako što se izmjeri vrijeme za koje voz pređe rastojanje od stuba do stuba, koje iznosi 1 km.

PROBLEM 33:

Kada se brže krećemo oko Sunca – danju ili noću?

Odgovor: Brže se krećemo noću nego danju – što se može zaključiti iz grafičkog prikaza brzine čovjeka na Ekvatoru u podne

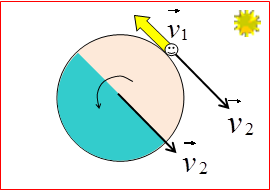
i brzine čovjeka na Ekvatoru u ponoć.

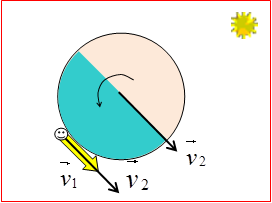
Brzina koju ima čovjek zbog kretanja centra Zemlje oko Sunca () i u podne i u ponoć ima isti smjer. Međutim, brzina koju čovjek ima zbog rotacije Zemlje oko svoje ose () u podne ima smjer suprotan smjeru brzine , a u ponoć isti smjer kao i brzina .

PROBLEM 34:

Ribolovac je kupio u prodavnici nit za štap za pecanje i želi da odredi kolika je maksimalna sila zatezanja koju nit može da izdrži. Na raspolaganju mu je teg od 1 kg i uglomjer. Odredite način na koji ribolovac može da odredi maksimalnu silu zatezanja.

Odgovor: Potrebno je okačiti teg o sredinu niti, a zatim vući kraj niti  u pravcu prikazanom strelicom (kao na slici).

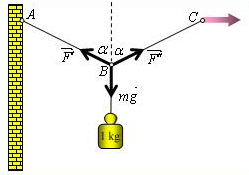
Za intenzitete sila na slici važi:

Odavde se dobija da je: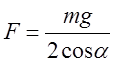

Kada postupno zatežemo nit, onda povećavamo vrijednost ugla α, a time i silu zatezanja niti F, sve dok ne dođe do njenog kidanja. Uglomjerom treba izmjeriti onaj ugao kada se kida nit.

Ako se nit kida čak i za , onda je treba udvostručiti i ponoviti opisani postupak. Naravno, ne treba zaboraviti da u ovom slučaju dobijenu vrijednost treba podijeliti sa dva.

PROBLEM 35:

Koliko bi trebalo da traje dan na Zemlji, da bi tijela na njenom Ekvatoru bila u bestežinskom stanju? Poluprečnik Zemlje na Ekvatoru je 6370 km.

Odgovor: Riješimo ovaj zadatak tako što ćemo kretanje posmatrati iz referentnog sistema vezanog za osu rotacije Zemlje, koji se približno može smatrati inercijalnim kada se zanemari kretanje Zemlje oko Sunca. U ovom sistemu tijelo kruži zahvaljujući postojanju stvarne, centripetalne sile.

Drugi Njutnov zakon za kretanje na Ekvatoru tijela mase m ima oblik:

gdje je  sila Zemljine teže, a  normalna reakcija podloge. Projekcija ove jednakosti na – osu ima oblik:

gdje je  centripetalno ubrzanje.

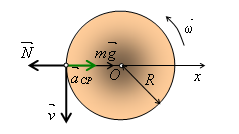
Težina tijela je po intenzitetu jednaka normalnoj reakciji podloge, odnosno:

U bestežinskom stanju j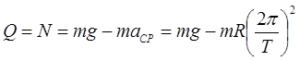e:

Tada je: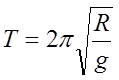 

PROBLEM 36:

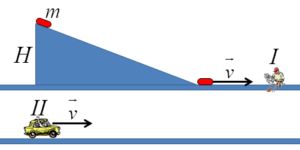
Tijelo mase m klizi niz glatku strmu ravan visine H. Za posmatrača I, koji miruje, potencijalna energija tijela prelazi u njegovu kinetičku energiju , tako da u podnožju strme ravni tijelo ima brzinu . Posmatrač II se kreće stalnom brzinom . Za njega, u početku kamen ima potencijalnu energiju  i kinetičku energiju , a na kraju ni jednu ni drugu.

Gdje je “nestala” njegova energija?

Zanemaruje se obrtanje Zemlje oko svoje ose i oko Sunca.

Odgovor: Ovaj primjer dobro ilustuje pogrešnu analizu fizičke pojave, odnosno pogrešan izbor fizičkog sistema: analiziran je nezatvoren sistem – tijelo, a Zemlja, sa kojom tijelo interaguje, nije uzeta u razmatranje.

1. a) U sistemu referencije vezanom za centar mase tijelo-Zemlja, u početnom trenutku tijelo i Zemlja miruju i mehanička energija jednaka je potencijalnoj energiji tijela. U konačnom trenutku tijelo se kreće brzinom 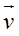 , a Zemlja brzinom  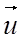, koju možemo naći iz zakona održanja impulsa 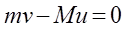: , odakle je  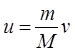, gdje je M– masa Zemlje.

Prema zakonu održanja mehaničke energije je:

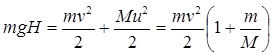
Pošto je m mnogo manje od M , onda m/M možemo da zanemarimo u poređenju s brojem jedan. Tada dobijamo da je: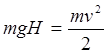 

što potpuno odgovara uslovima zadatka.

1. b) Za posmatrača II, u početnom trenutku mehanička energija sistema je 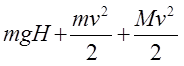 , a u konačnom .

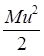Iz zakona održanja impulsa je:

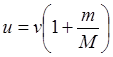
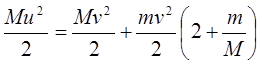
Tako, iz zakona održanja energije imamo da je:

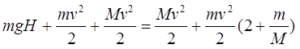
ili, zanemarujući vrijednost m/M u poređenju s brojem dva,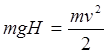 

što je isti rezultat kao i za posmatrača I.

PROBLEM 37:

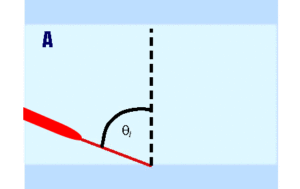
Odrediti ugao prelamanja b svjetlosnog zraka pri prelazu iz vode u vazduh ako je upadni ugao a + 60^o. Indeks prelamanja vose je n+1,33.

n1 sin a =n2 sinb

n sin a = sin b

sin b = 1,15 > 1

Kako je moguće primjenom fizičkog zakona da se dobije matematički apsurdan rezultat?

a_g = 49^o

Dekart-Snelijusov zakon prelamanja primijenjen u slučaju totalne refleksije

PROBLEM 38:

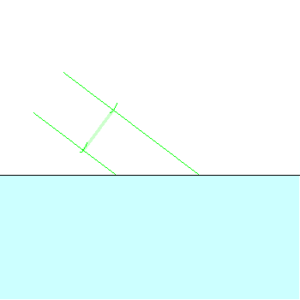
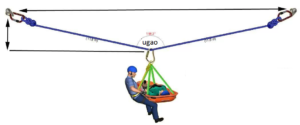
Treba izvući automobil iz jarka na cestu. Jedan kraj sajle privezali su za automobil, a drugi kraj za stablo pokraj puta. Sajlu su dobro zategli i gurali sredinu sajle u pravcu normalnom na njen pravac. Automobil se pokrenuo. Ponovo su zategli sajlu i ponovili postupak guranja sredine sajle.

Kako su uspjeli izvući iz jarka teški automobil sa relativno malom silom?

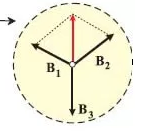Dva  vektora se mogu zamijeniti jednim (rezultujućim).

Jedan (rezultujući) vektor se može razložiti na dva vektora.

Odje se relativno mala sila razlaže na dvije sile (na drvo i na automobil) koje u početnom trenutku međusobno zaklapaju ugao malo manji od 180^o. Slika ispod pokazuje sličan primjer.

PROBLEM 39:

Tijelo je izbačeno vertikalno uvis početnom brzinom 20 m/s.

Koliki put pređe tijelo za 4 s? Kako je moguće da tijelo u toku 4 s ponovo nađe na istom mjestu sa kog je izbačeno?

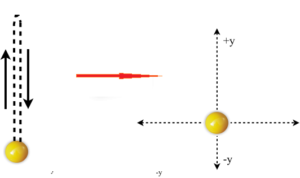Odgovor: Tijelo se kreće veritkalno naviše jednakousporeno (usporava ga ubrzanje zemljine teže) i za polovinu vremena od 4s dostigne maksimalnu visinu . Vrijeme penjanja možemo naći iz uslova da je na  maksimalnoj visni trenutna brzina jednaka nuli .

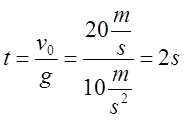
Maksimalna visina na koju se tijelo popelo za 2s se može izračunati:

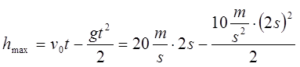
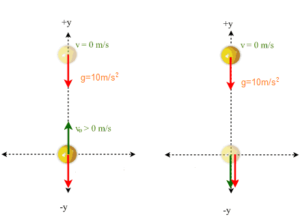
Nakon što dostigne maksimalnu visinu tijelo se vraća na zemlju kao slobodan pad (jednakobrzano kretanje bez početne brzine), kad pređe maksimalnu visinu h=20m, vraća se na zemlju za:

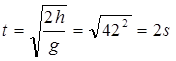Ukupni put H vertikalnog htica i slobodnog pada ; H= 2 x h=40m.

Ukupno vrijeme kretanja je 4s.

Nakon 4s tijelo će se vratiti na isto mjesto sa kog je izbačeno, zbog ubrzanja sile zemljine teže koja ga tokom penjanja usporava u jednom trenutku zaustavi, zatim ga ubrzanje g ‘natjera’ da se vrati na zemlju.